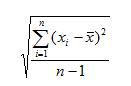In the last post, we covered the Normal distribution as it relates to the standard deviation. We said that the Normal distribution is really a family of unimodal, symmetric distributions that differ only by their means and standard deviations. Now is a good time to introduce a new term: Parameter. When dealing with perfect-world models like the Normal model, their major measures -- in this case, their mean and standard deviation -- are called parameters. The mean (denoted by the Greek letter "mu" (pronounced "mew"), µ, and the standard deviation is denoted by the Greek letter sigma, σ. We can refer to a particular normal model by identifying µ and σ and using the letter N, for "Normal:" N(µ, σ). For example, if I want to describe a Normal model whose mean is 14 and whose standard deviation is 2, I use the notation N(14, 2).
Every Normal model has some pretty interesting properties, which we will now cover. Take the above model N(14,2). We'll draw it on a number line centered at 14, with units of 2 marked off in either direction. Each unit of 2 is one standard deviation in length. It would look like this...
Now let's mark off the area that's between 12 and 16; that is, the area that's within one standard deviation of the mean. In a Normal model, this region will contain 68% of the data values:
If you've ever heard of "grading on a curve," it's based on Normal models. Scores within one standard deviation of the mean would generally be considered in the "C" grade range.
Now, if you consider the region that lies within two standard deviations from the mean; that is, between 10 and 18 in this model, this area would encompass 95% of all the data values in the data set:
From a grading curve standpoint, 95% of the values would be Bs or Cs. Finally, if you mark off the area within 3 standard deviations from the mean, this region will contain about 99.7% of the values in the data set. These extremities would be the As and Fs in our grading curve interpretation.
In statistics, this percentage breakdown is called the "Empirical Rule," or the "68-95-99.7 Rule."
What about the regions up to 8 and beyond 20? These areas account for the remaining 0.3% of the data values? That would make 0.15% on each side.
(Self-Test): What percent of data values lie between 12 and 14 in N(14,2) above?
(Answer): If 68% represents the full area between 12 and 16 and given that the Normal model is perfectly symmetric, there must be half of 68%, or 34% between 12 and 14. Likewise, there would be 34% between 14 and 16.
(Self-Test): What percent of data values lie between 16 and 18 in N(14,2) above?
(Answer): Subtract 95% minus 68% = 27%. This represents the number of data values between 10 and 12, and between 16 and 18 both. Divide by 2 and you get 13.5% in each of these regions.
If you do similar operations, the various areas break down like the following:
(Self-Test): In any Normal model what percent of data values are greater than 2 standard deviations from the mean?
(Answer): Using the above model, the question is asking for the percent of data values that are more than 18. You would add the 2.35% and the 0.15% to get the answer: 2.50%.
This is all well and good if you're looking at areas that involve a whole number of standard deviations, but what about all the in-between numbers? For example, what if you wanted to know what percent of data values are within 1.5 standard deviations of the mean? This will be the subject of a future post.
What is Statistics? Why is it one of the most misunderstood, misused, and underappreciated mathematics fields? Read on to learn basic statistics and see it in action!
How's it going so far?
Wednesday, August 31, 2011
Saturday, August 27, 2011
More About Standard Deviation: The Normal Distribution
I've haven't said a lot about Standard Deviation up to now: not much more than the fact that it's a measure of spread for a symmetric dataset. However, we can also think of the standard deviation as a unit of measure of relative distance from the mean in a unimodal, symmetric distribution.
Suppose you had a perfectly symmetric, unimodal distribution. It would look like the well-known bell curve. Of course, in the real world, nothing is perfect. But in statistics, we talk about ideal distributions, known as "models." Real-life datasets can only approximate the ideal model...but we can apply many of the traits of models to them.
So let's talk about a perfectly symmetric, bell-shaped distribution for a bit. We call this model a Normal distribution, or Normal model. Because we're dealing with perfection, the mean and median are at the same point. In fact, there are an infinite number of Normal distributions with a particular mean. They only differ in width. Below are some examples of Normal models.
Notice that their widths differ. Another word for "width" is "spread"...which brings us back to Standard Deviation! Take a look at the curves above. In the center section, the shape looks like an upside down bowl, whereas the outer "legs" look like part of a right-side-up bowl. Now imagine the point at which the right-side-up parts meet the upside-down part. Look below for the two blue dots in the diagram. (P.S. They are called "points of inflection," in case you were wondering.)
As shown above, if a line is drawn down the center, the distance from that line to a blue point is the length of one standard deviation. Can you see which lengths of standard deviations in the earlier examples are larger? Smaller?
So, there are two measures that define how a particular Normal model will look: the mean and the standard deviation.
I'd be remiss if I didn't tell you that there is a formula for numerically finding the standard deviation. Luckily, there's a lot of technology out there that automatically computes this for you. (I showed you how to do this in MS-Excel in an earlier post.)
Suppose you have a list of "n" data values, and when you look at a histogram of these values, you see that the distribution is unimodal and roughly symmetric. If we call the values x1, x2, x3, etc. We compute the mean (average, remember?) and note it as x with a bar over it. Then the formula is:
Suppose you had a perfectly symmetric, unimodal distribution. It would look like the well-known bell curve. Of course, in the real world, nothing is perfect. But in statistics, we talk about ideal distributions, known as "models." Real-life datasets can only approximate the ideal model...but we can apply many of the traits of models to them.
So let's talk about a perfectly symmetric, bell-shaped distribution for a bit. We call this model a Normal distribution, or Normal model. Because we're dealing with perfection, the mean and median are at the same point. In fact, there are an infinite number of Normal distributions with a particular mean. They only differ in width. Below are some examples of Normal models.

Notice that their widths differ. Another word for "width" is "spread"...which brings us back to Standard Deviation! Take a look at the curves above. In the center section, the shape looks like an upside down bowl, whereas the outer "legs" look like part of a right-side-up bowl. Now imagine the point at which the right-side-up parts meet the upside-down part. Look below for the two blue dots in the diagram. (P.S. They are called "points of inflection," in case you were wondering.)
As shown above, if a line is drawn down the center, the distance from that line to a blue point is the length of one standard deviation. Can you see which lengths of standard deviations in the earlier examples are larger? Smaller?
So, there are two measures that define how a particular Normal model will look: the mean and the standard deviation.
I'd be remiss if I didn't tell you that there is a formula for numerically finding the standard deviation. Luckily, there's a lot of technology out there that automatically computes this for you. (I showed you how to do this in MS-Excel in an earlier post.)
Suppose you have a list of "n" data values, and when you look at a histogram of these values, you see that the distribution is unimodal and roughly symmetric. If we call the values x1, x2, x3, etc. We compute the mean (average, remember?) and note it as x with a bar over it. Then the formula is:
What does the ∑ mean? Let's take the formula apart. First, you are finding the difference between each data value and the mean of the whole dataset. You're squaring it to make sure you're dealing only with positive values. The ∑ means you should add up all those positive squared answers, one for each value in your dataset. Once you have the sum, you divide by
(n-1), which gives you an average of all the squared differences from the mean. This measure (before taking the square root) is called the variance. When you take the square root, you have the value of the standard deviation. So, you see, the standard deviation is the square root of the squared differences from the mean.
Well, that's a lot to digest, so I'll continue with the properties of the Normal model in my next post.
Labels:
bell curve,
mean,
median,
model,
Normal distribution,
Normal model,
points of inflection,
standard deviation,
variance
Saturday, August 20, 2011
Analyzing Quantitative Distributions
This post deals only with quantitative data.
When you have a quantitative dataset, it is always a good idea to look at a graphical display of it: usually a histogram or boxplot, although there are others. What you are looking to describe is the shape of the data (the subject of a recent post), the approximate center of the dataset, the spread of the values, and any unusual features (such as extremely low or high values -- outliers). We'll take them one at a time.
Shape
The shape of the dataset helps us determine how to report on the other features. We went into detail about shape in a very recent post ("The Shape of a Quantitative Distribution"). If the display is basically symmetric, you will use the mean to describe the center and a measure called the Standard deviation to describe the spread. If the display is non-symmetric, you will use the median to describe the center and the interquartile range to describe the spread. Here's a handy chart to summarize this.
Center
In a symmetric distribution the mean and median are at approximately the same place; however, statisticians use the mean. In a non-symmetric distribution, the median is used because by its very definition, it is not calculated using any extreme points or points that skew the calculation.
Spread
Notice that the range (which is the difference between the largest and smallest data value in the set) is not generally used to describe the spread. In a symmetric distribution we use the standard deviation, which has a complicated formula but a simple description: the Standard Deviation is the average squared difference between each value in the dataset and the mean of the dataset. You can find the standard deviation using a graphing calculator or a tool like MS-Excel. The symbol for Standard Deviation is
Standard deviations are relative. By that I mean that you can't tell just by looking at its value whether it's large or small -- it depends on the values in the dataset. Standard deviations are good for comparing spreads if you have two distributions. And, we'll soon find out that the standard deviation has an extremely important use in statistics. Here's an example for finding the mean and standard deviation using MS-Excel:
In a non-symmetric distribution we use the Interquartile Range (IQR) because this tells the spread of the central 50% of the data values. Like the median, the IQR isn't influenced by outliers or skewness. Here's an example of finding the median and IQR using MS-Excel:
Unusual Features
As mentioned above, unusual features include extreme points (if any), also known as outliers. In an earlier post, we covered how to determine the boundaries for outliers. If a data value lies outside the boundaries, we call it an outlier. If a value isn't quite an outlier but close, it's worth mentioning in a description of a distribution. Just call it an "extreme point."
When you have a quantitative dataset, it is always a good idea to look at a graphical display of it: usually a histogram or boxplot, although there are others. What you are looking to describe is the shape of the data (the subject of a recent post), the approximate center of the dataset, the spread of the values, and any unusual features (such as extremely low or high values -- outliers). We'll take them one at a time.
Shape
The shape of the dataset helps us determine how to report on the other features. We went into detail about shape in a very recent post ("The Shape of a Quantitative Distribution"). If the display is basically symmetric, you will use the mean to describe the center and a measure called the Standard deviation to describe the spread. If the display is non-symmetric, you will use the median to describe the center and the interquartile range to describe the spread. Here's a handy chart to summarize this.
Center
In a symmetric distribution the mean and median are at approximately the same place; however, statisticians use the mean. In a non-symmetric distribution, the median is used because by its very definition, it is not calculated using any extreme points or points that skew the calculation.
Spread
Notice that the range (which is the difference between the largest and smallest data value in the set) is not generally used to describe the spread. In a symmetric distribution we use the standard deviation, which has a complicated formula but a simple description: the Standard Deviation is the average squared difference between each value in the dataset and the mean of the dataset. You can find the standard deviation using a graphing calculator or a tool like MS-Excel. The symbol for Standard Deviation is
Standard deviations are relative. By that I mean that you can't tell just by looking at its value whether it's large or small -- it depends on the values in the dataset. Standard deviations are good for comparing spreads if you have two distributions. And, we'll soon find out that the standard deviation has an extremely important use in statistics. Here's an example for finding the mean and standard deviation using MS-Excel:
In a non-symmetric distribution we use the Interquartile Range (IQR) because this tells the spread of the central 50% of the data values. Like the median, the IQR isn't influenced by outliers or skewness. Here's an example of finding the median and IQR using MS-Excel:
Unusual Features
As mentioned above, unusual features include extreme points (if any), also known as outliers. In an earlier post, we covered how to determine the boundaries for outliers. If a data value lies outside the boundaries, we call it an outlier. If a value isn't quite an outlier but close, it's worth mentioning in a description of a distribution. Just call it an "extreme point."
Labels:
center,
interquartile range,
IQR,
outliers,
shape,
spread,
standard deviation
Tuesday, August 16, 2011
The Shape of a Quantitative Distribution
When you graph quantitative data, you can often see some kind of shape emerge. Here are some typical block structures that illustrate some possible shapes a display might take. We call the set of values "distributions."
(Self-Test): Which three of the above graphs look symmetric?
(Answer): B, D, and E.
The next thing you might notice is that some graphs have peaks whereas others look pretty level. We call the peaks "modes." If there's one peak, we say the graph has a unimodal distribution. If there are two peaks, the graph has a bimodal distribution.
(Self-Test): Which three of the above graphs look unimodal? Which is bimodal?
(Answer): A, B, and C are unimodal; D is bimodal.
FYI, a graph that's mostly level-looking, like graph E, is called uniform.
Now take a look at distributions A and C. Do you see that each has a "tail" at one end? When a distribution is off-center (compared to graph B), we say it is skewed. The direction of the tail is the direction of the skewness. For example, graph A is skewed left because the tail is on the left side of the graph. graph C is skewed right.
When we describe a distribution we try to describe its shape, center, and spread, plus anything unusual about it, such as outliers. This will be the subject of my next post.
(Self-Test): Which of the distributions pictured above might have outliers?
(Answer): Skewed graphs, like A and C, depending on the length of their tails. The longer the tail, the more likely there are outliers.
The first thing you need to determine is if there is any symmetry to the graph. If you were to visualize a vertical line going down the center, does each side look like a mirror image of the other? No real-life distribution will be perfectly symmetrical, but if it's close, it's worth mentioning.
(Answer): B, D, and E.
The next thing you might notice is that some graphs have peaks whereas others look pretty level. We call the peaks "modes." If there's one peak, we say the graph has a unimodal distribution. If there are two peaks, the graph has a bimodal distribution.
(Self-Test): Which three of the above graphs look unimodal? Which is bimodal?
(Answer): A, B, and C are unimodal; D is bimodal.
FYI, a graph that's mostly level-looking, like graph E, is called uniform.
Now take a look at distributions A and C. Do you see that each has a "tail" at one end? When a distribution is off-center (compared to graph B), we say it is skewed. The direction of the tail is the direction of the skewness. For example, graph A is skewed left because the tail is on the left side of the graph. graph C is skewed right.
When we describe a distribution we try to describe its shape, center, and spread, plus anything unusual about it, such as outliers. This will be the subject of my next post.
(Self-Test): Which of the distributions pictured above might have outliers?
(Answer): Skewed graphs, like A and C, depending on the length of their tails. The longer the tail, the more likely there are outliers.
Labels:
bimodal,
center,
distribution,
mode,
shape,
skewed,
skewed left,
skewed right,
skewness,
spread,
symmetric,
uniform,
unimodal
Sunday, August 14, 2011
Picturing Quantitative Data
Just in case you didn't read the post "Picturing Categorical Data," here's a tiny bit of rehash: The first thing to note that different types of data are pictured in different ways. You might recall from an earlier posting that there are two types of data:
There are many ways to picture quantitative data, but let me introduce two that are most used: the boxplot and the histogram. In both cases, let's use the following set of scores, which are arranged in descending order.
Boxplots
(Self-Test): In the earlier post, entitled "Percentiles and Quartiles," we discussed the 5 number summary, consisting of which 5 measures?
A boxplot uses these 5 numbers, arranged on a number line according to their values. As we discussed, each of the four regions marked off by these 5 numbers contain 1/4 of the values in the data set, even if they don't have the same width.
There are 21 numbers shown above. The minimum is 72 and the maximum is 98. Since the number are arranged numerically, we can count to the 11th number to find the median: 85.
We now have 10 numbers on each side of the median. The 1st and 3rd quartiles are the medians of the lower 10 and upper 10 numbers, respectively. Q1 is 75, and Q3 is midway between 90 and 91. Remember: just look between the 5th and 6th number from the bottom and the top in each case.
So, our 5-number summary is: 72 (min), 75 (Q1), 85 (median), 90.5 (Q3), and 98 (max). To make a boxplot, draw a number line that stretches from, say, 70 to 100 and place the 5 numbers in their proper places. Then draw a box around the middle 3 numbers to show the span of the middle 50% of the number set:
A boxplot is helpful not only to see the spread of the data set, but also to see the symmetry of the data. For example, the stretch between the minimum and the median is about the same size as the stretch between the median and the maximum, which tells us that the mean lines up pretty well with the median. (Recall that it doesn't always end up this way!) The unevenness of the outer regions (which we call the "whiskers") are uneven, telling us that the data looks more heavily weighted toward the low side of the number line. If the boxplot looked like the following, the data would be roughly symmetric:
Now, if a data set has outliers, they are shown with a symbol; for instance, a star:
In cases like this, a new maximum that lies within the boundary for outliers is determined. As I said in a previous post, you should look for possible reasons for outliers.
Histograms
A histogram tracks the number of observations (like the values in the above table) that lie within consecutive, same-width intervals on a number line. While most people do not make histograms by hand, we'll go through how it's done so you can understand what a histogram looks like. In statistics histograms are used heavily; usually to see the shape of the data distribution.
Start by examining the data values. They range from 72 to 98, and the range (as defined in statistics) is 98 - 72 or 26. We want to divide 26 into a number of equal-sized intervals, then find out how many of the numbers in the data set lie in each interval. We will represent that number as the height of that interval's bar.
How many intervals do we need? Well, to me, that's a "squishy" question. You want enough to be able to see a shape, but not so many that you hardly have any values in each interval. A rule of thumb that I use is between 6 and 8. Because our range is 26, I'm going to use 7 for intervals, because 7*4 is 28, which is closer to 26 than a multiple of 6 or 8. So we have the following number line. Each interval will be 4 units wide (again, because 7*4 is 28), so I've numbered the line accordingly.
(Self-Test): What's with the // on the number line above?
(Answer): Number lines should always be to scale, but in this case a number line going from 0 to 100 probably wouldn't fit on the page. So, I use the // to indicate a break in the numbering.
Now I need to make a small decision: Shall I count the labelled numbers as the start or the end of the interval? It doesn't matter, just as long as you're consistent. I'm going to count the numbers as the start of each interval. So, my first interval will go from 72 to 75; my second will be from 76 to 79, and so on.
For each interval, you need to count how many values in the data set fall within that interval. For example, there are 6 numbers that are between 72 and 75, inclusive. So the height of my bar for the first interval will be 6 units high.
Our second interval, which goes from 76 to 79, has no values. So we leave a space to show that zero values are in that interval. The next interval goes from 80 to 83, and there are four values that lie in that interval. So, the bar will be 4 units high.
Continuing on for the rest of the intervals, here is our finished product:
This histogram has an interesting shape. If the dataset represents grades, we can assume that there 6 out of 21 "C" students, while twice that many are in the "B" to "A-" range. I'll be saying more about shapes of distributions in a later post. For now, suffice it to say that the shape of a distribution is an important thing to assess when you're looking at data.
- Quantitative data are numbers for which it makes sense to do arithmetic on them. For example, test scores, dollars, miles, etc. it is meaningful to, say, find their average. Quantitative data usually have labels.
- Categorical data are sub-levels of variables that you do not combine with arithmetic. You usually count them. Examples: eye colors (bllue, brown, green, hazel), education levels (high school, undergrad, graduate, etc.). Some categorical variables are numbers, but not ones that make sense to add; examples are zip codes, numbers on athletic jerseys, phone numbers.
There are many ways to picture quantitative data, but let me introduce two that are most used: the boxplot and the histogram. In both cases, let's use the following set of scores, which are arranged in descending order.
98 | 86 | 81 |
95 | 86 | 75 |
92 | 86 | 75 |
91 | 85 | 75 |
91 | 82 | 74 |
90 | 82 | 73 |
89 | 81 | 72 |
A boxplot uses these 5 numbers, arranged on a number line according to their values. As we discussed, each of the four regions marked off by these 5 numbers contain 1/4 of the values in the data set, even if they don't have the same width.
There are 21 numbers shown above. The minimum is 72 and the maximum is 98. Since the number are arranged numerically, we can count to the 11th number to find the median: 85.
We now have 10 numbers on each side of the median. The 1st and 3rd quartiles are the medians of the lower 10 and upper 10 numbers, respectively. Q1 is 75, and Q3 is midway between 90 and 91. Remember: just look between the 5th and 6th number from the bottom and the top in each case.
So, our 5-number summary is: 72 (min), 75 (Q1), 85 (median), 90.5 (Q3), and 98 (max). To make a boxplot, draw a number line that stretches from, say, 70 to 100 and place the 5 numbers in their proper places. Then draw a box around the middle 3 numbers to show the span of the middle 50% of the number set:
A boxplot is helpful not only to see the spread of the data set, but also to see the symmetry of the data. For example, the stretch between the minimum and the median is about the same size as the stretch between the median and the maximum, which tells us that the mean lines up pretty well with the median. (Recall that it doesn't always end up this way!) The unevenness of the outer regions (which we call the "whiskers") are uneven, telling us that the data looks more heavily weighted toward the low side of the number line. If the boxplot looked like the following, the data would be roughly symmetric:
Symmetry in a data set is important to recognize, because we can assume other important traits. More about this in a future post.
Now, if a data set has outliers, they are shown with a symbol; for instance, a star:
In cases like this, a new maximum that lies within the boundary for outliers is determined. As I said in a previous post, you should look for possible reasons for outliers.
Histograms
A histogram tracks the number of observations (like the values in the above table) that lie within consecutive, same-width intervals on a number line. While most people do not make histograms by hand, we'll go through how it's done so you can understand what a histogram looks like. In statistics histograms are used heavily; usually to see the shape of the data distribution.
Start by examining the data values. They range from 72 to 98, and the range (as defined in statistics) is 98 - 72 or 26. We want to divide 26 into a number of equal-sized intervals, then find out how many of the numbers in the data set lie in each interval. We will represent that number as the height of that interval's bar.
How many intervals do we need? Well, to me, that's a "squishy" question. You want enough to be able to see a shape, but not so many that you hardly have any values in each interval. A rule of thumb that I use is between 6 and 8. Because our range is 26, I'm going to use 7 for intervals, because 7*4 is 28, which is closer to 26 than a multiple of 6 or 8. So we have the following number line. Each interval will be 4 units wide (again, because 7*4 is 28), so I've numbered the line accordingly.
(Self-Test): What's with the // on the number line above?
(Answer): Number lines should always be to scale, but in this case a number line going from 0 to 100 probably wouldn't fit on the page. So, I use the // to indicate a break in the numbering.
Now I need to make a small decision: Shall I count the labelled numbers as the start or the end of the interval? It doesn't matter, just as long as you're consistent. I'm going to count the numbers as the start of each interval. So, my first interval will go from 72 to 75; my second will be from 76 to 79, and so on.
For each interval, you need to count how many values in the data set fall within that interval. For example, there are 6 numbers that are between 72 and 75, inclusive. So the height of my bar for the first interval will be 6 units high.
Our second interval, which goes from 76 to 79, has no values. So we leave a space to show that zero values are in that interval. The next interval goes from 80 to 83, and there are four values that lie in that interval. So, the bar will be 4 units high.
Continuing on for the rest of the intervals, here is our finished product:
This histogram has an interesting shape. If the dataset represents grades, we can assume that there 6 out of 21 "C" students, while twice that many are in the "B" to "A-" range. I'll be saying more about shapes of distributions in a later post. For now, suffice it to say that the shape of a distribution is an important thing to assess when you're looking at data.
Labels:
5-number summary,
box-and-whisker plot,
boxplot,
histogram,
maximum,
median,
minimum,
quartile,
range,
whisker
Friday, August 12, 2011
Keeping it Simple -- the Area Principle
If you made it through the [rather long] post entitled "Picturing Categorical Data," this next post brings out a fine point about making graphical displays. If you look through articles and newspapers, or perhaps at slides that people make in your office for presentations, you might see a tendency for folks to want to make them fancy. While this is admirable -- trying to show potentially dry information in a more splashy way -- it can end up being misleading. Read on.
Take a look at this pie chart, which graphs quantities that are 10%, 20%, 30%, and 40% of the whole.
Now compare it to its flashy 3-D counterpart:
"What's the difference?" you might ask. However, I would argue that the 3-D version makes the green slice (30%) look larger than the purple (40%) slice. Can you see it? This doesn't always happen with 3-D displays, but 3-D displays are prone to this. It's something that you want to look out for, just in case.
When a smaller pie slice or bar (in a bar chart) looks larger than a slice or bar that represents a larger quantity, we say that the display violates the Area Principle. In the first display, each piece was proportionately sized relative to the others.
Why make this point? When trying to communicate something graphically, the main point is to get the information across with as little potential confusion as possible -- not to impress people with fancy pictures. Statistics can be mind-boggling to many, so why not try to make things as straightforward as possible? It's the old K.I.S.S. principle. Statistics-challenged people will thank you! (As I'm sure you're thanking me for the short post!)
Take a look at this pie chart, which graphs quantities that are 10%, 20%, 30%, and 40% of the whole.
Now compare it to its flashy 3-D counterpart:
"What's the difference?" you might ask. However, I would argue that the 3-D version makes the green slice (30%) look larger than the purple (40%) slice. Can you see it? This doesn't always happen with 3-D displays, but 3-D displays are prone to this. It's something that you want to look out for, just in case.
When a smaller pie slice or bar (in a bar chart) looks larger than a slice or bar that represents a larger quantity, we say that the display violates the Area Principle. In the first display, each piece was proportionately sized relative to the others.
Why make this point? When trying to communicate something graphically, the main point is to get the information across with as little potential confusion as possible -- not to impress people with fancy pictures. Statistics can be mind-boggling to many, so why not try to make things as straightforward as possible? It's the old K.I.S.S. principle. Statistics-challenged people will thank you! (As I'm sure you're thanking me for the short post!)
Wednesday, August 10, 2011
Has the Stock Market Hit Bottom?
Oh, if only there were a nice statistical way to answer that question! In the August 10, 2011 issue of USA Today, the article at http://www.usatoday.com/money/markets/2011-08-09-has-market-hit-bottom_n.htm offered a lot of insights from experts, but the authors were wise enough to know that there’s just no telling whether the stock market will rise or fall, or whether better days are to come yet.
For anyone who’s not aware, the Dow Jones Industrial average (DJIA) plummeted 535 points on Monday, following the bad news that the US credit rating had dropped from AAA to AA+, according to Standard & Poors and probably a multitude of other events that stripped investors of their confidence. The following day, August 9, the DJIA gained back 435 points, bringing it closer to pre-plummet levels. At this writing (Wednesday, August 10, 2011 at 1:35 p.m.), the Dow is down about 357 points.
The insights offered by experts as to why the market is plummeting range from emotional sell-offs in light of the US credit rating downgrade, to the state of theoverall world economy, to the lack of warm fuzzies in Congress, but no one is making a the mistake of trying to predict the future. Nothing, not even statistics, can do that reliably.
Theoretically, even if somehow we were able to identify *all* of the factors (“variables” we call them) that make for fluctuations in the stock market, and then we found some realistic way to quantify each of the factors, we could come up with a [probably quite complicated] equation involving all of those variables that we could use to predict future behavior, but it would be just that – a prediction. You simply cannot use statistics to foretell the future. The best one can do is make a fact-based, educated guess.
Similarly, you cannot use the past to predict the future. Most of fall into this trap pretty easily. For example, a lot of people moved their investments to Treasury-related securities, because Treasury issues have shown a steadily upward trend without the volatility of riskier investments, like stocks. In fact, in the past 10 years, inflation-protected securities (TIPS) have out-performed the Dow, the Nasdaq, and the S&P 500 significantly…at about half the risk (as rated by Vanguard). So are you rushing to your favorite investment site to move your money? If you are, then you’re using past performance to predict the future! Sometimes it works, but just as often it doesn’t.
Has the stock market hit bottom? Read the article, and you be the judge. Just trying to set your expectations about what statistics can and cannot do!
Sunday, August 7, 2011
Picturing Categorical Data
They say a picture is worth a thousand words, and that's certainly true with statistical data! The first thing to note that different types of data are pictured in different ways. You might recall from an earlier posting that there are two types of data:
There are two ways to "graphically" picture categorical data: bar charts and pie charts. You see these all the time in articles. Let's use the following base data that shows eye colors in a group of 115 people:
Bar Charts
The most straightforward type of display is a bar chart. Bar charts can portray the actual numbers...
...or they can portray percents of the whole (115)...
Notice that the bars can be vertical or horizontal. In either case, the bars are arranged in either increasing or decreasing size.
If you have a number of very small bars, you can put them together as a larger combined bar and label it "Other." Such bars don't necessarily need to be placed in order; they usually appear as the last bar. Suppose, for example, you want to put green, hazel, and gray together as an "Other" bar. Then your graph would look like this:
Sometimes you will see a single bar with sections representing each category in proportion. This is called a segmented (or stacked) bar chart. They can appear with the actual counts (height of the single bar is equal to the sum of the counts), or as percentages (height of the single bar represents 100%). Here's how a segmented bar chart with percents would look. Notice that it's good to arrange the bars in decreasing order from bottom to top:
Segmented bar charts are especially helpful in comparing the same categories in two or more different groups. Suppose we had a second group of people whose segmented bar chart of eye colors looked slightly different. We could put the bars side by side in a single display, with the eye colors in the same order.
It is easy to see that there are fewer brown-eyed people in Group 2, but more blue-eyed people, about the same number of green and gray eyed-people, but fewer with hazel eyes.
One caution with two or more segmented bars: Unless each group is exactly the same size, you should use percents rather than counts. Otherwise it would be nearly impossible to compare the bars.
Pie Charts
A pie chart shows each category as a proportional-sized pie slice. Pie charts always use percents. So, a pie chart for our eye color data would look like this:
Notice that the pieces are arranged in order of size as you go around the pie.
(Self-Test): Suppose there's another group -- this time consisting of 140 people -- whose eye colors are as follows. Make a "Group 3" segmented bar chart to show the differences.
(Answer): See below.
- Categorical data are sub-levels of variables that you do not combine with arithmetic. You usually count them. Examples: eye colors (bllue, brown, green, hazel, gray), education levels (high school, undergrad, graduate, etc.). Some categorical variables are numbers, but not ones that make sense to add; examples are zip codes, numbers on athletic jerseys, and phone numbers.
- Quantitative data are numbers for which it makes sense to do arithmetic on them. For example, with test scores, dollars, miles, etc., it is meaningful to, say, find their average. Quantitative data usually have labels.
There are two ways to "graphically" picture categorical data: bar charts and pie charts. You see these all the time in articles. Let's use the following base data that shows eye colors in a group of 115 people:
Bar Charts
The most straightforward type of display is a bar chart. Bar charts can portray the actual numbers...
...or they can portray percents of the whole (115)...
Notice that the bars can be vertical or horizontal. In either case, the bars are arranged in either increasing or decreasing size.
If you have a number of very small bars, you can put them together as a larger combined bar and label it "Other." Such bars don't necessarily need to be placed in order; they usually appear as the last bar. Suppose, for example, you want to put green, hazel, and gray together as an "Other" bar. Then your graph would look like this:
Sometimes you will see a single bar with sections representing each category in proportion. This is called a segmented (or stacked) bar chart. They can appear with the actual counts (height of the single bar is equal to the sum of the counts), or as percentages (height of the single bar represents 100%). Here's how a segmented bar chart with percents would look. Notice that it's good to arrange the bars in decreasing order from bottom to top:
Segmented bar charts are especially helpful in comparing the same categories in two or more different groups. Suppose we had a second group of people whose segmented bar chart of eye colors looked slightly different. We could put the bars side by side in a single display, with the eye colors in the same order.
It is easy to see that there are fewer brown-eyed people in Group 2, but more blue-eyed people, about the same number of green and gray eyed-people, but fewer with hazel eyes.
One caution with two or more segmented bars: Unless each group is exactly the same size, you should use percents rather than counts. Otherwise it would be nearly impossible to compare the bars.
Pie Charts
A pie chart shows each category as a proportional-sized pie slice. Pie charts always use percents. So, a pie chart for our eye color data would look like this:
Notice that the pieces are arranged in order of size as you go around the pie.
(Self-Test): Suppose there's another group -- this time consisting of 140 people -- whose eye colors are as follows. Make a "Group 3" segmented bar chart to show the differences.
(Answer): See below.
Subscribe to:
Posts (Atom)