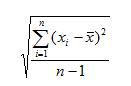More About the Normal Distribution: the 68-95-99.7 Rule

In the last post, we covered the Normal distribution as it relates to the standard deviation. We said that the Normal distribution is really a family of unimodal, symmetric distributions that differ only by their means and standard deviations. Now is a good time to introduce a new term: Parameter. When dealing with perfect-world models like the Normal model, their major measures -- in this case, their mean and standard deviation -- are called parameters. The mean (denoted by the Greek letter "mu" (pronounced "mew"), µ, and the standard deviation is denoted by the Greek letter sigma, σ. We can refer to a particular normal model by identifying µ and σ and using the letter N, for "Normal:" N(µ, σ). For example, if I want to describe a Normal model whose mean is 14 and whose standard deviation is 2, I use the notation N(14, 2).

Every Normal model has some pretty interesting properties, which we will now cover. Take the above model N(14,2).  We'll draw it on a number line centered at 14, with units of 2 marked off in either direction. Each unit of 2 is one standard deviation in length. It would look like this...

Now let's mark off the area that's between 12 and 16; that is, the area that's within one standard deviation of the mean. In a Normal model, this region will contain 68% of the data values:

If you've ever heard of "grading on a curve," it's based on Normal models. Scores within one standard deviation of the mean would generally be considered in the "C" grade range.

Now, if you consider the region that lies within two standard deviations from the mean; that is, between 10 and 18 in this model, this area would encompass 95% of all the data values in the data set:

From a grading curve standpoint, 95% of the values would be Bs or Cs. Finally, if you mark off the area within 3 standard deviations from the mean, this region will contain about 99.7% of the values in the data set. These extremities would be the As and Fs in our grading curve interpretation.

In statistics, this percentage breakdown is called the "Empirical Rule," or the "68-95-99.7 Rule."

What about the regions up to 8 and beyond 20? These areas account for the remaining 0.3% of the data values? That would make 0.15% on each side.

(Self-Test): What percent of data values lie between 12 and 14 in N(14,2) above?
(Answer): If 68% represents the full area between 12 and 16 and given that the Normal model is perfectly symmetric, there must be half of 68%, or 34% between 12 and 14. Likewise, there would be 34% between 14 and 16.

(Self-Test): What percent of data values lie between 16 and 18 in N(14,2) above?
(Answer): Subtract 95% minus 68% = 27%. This represents the number of data values between 10 and 12, and between 16 and 18 both. Divide by 2 and you get 13.5% in each of these regions.

If you do similar operations, the various areas break down like the following:

(Self-Test): In any Normal model what percent of data values are greater than 2 standard deviations from the mean?
(Answer): Using the above model, the question is asking for the percent of data values that are more than 18. You would add the 2.35% and the 0.15% to get the answer: 2.50%.

This is all well and good if you're looking at areas that involve a whole number of standard deviations, but what about all the in-between numbers? For example, what if you wanted to know what percent of data values are within 1.5 standard deviations of the mean? This will be the subject of a future post.

More About Standard Deviation: The Normal Distribution

I've haven't said a lot about Standard Deviation up to now: not much more than the fact that it's a measure of spread for a symmetric dataset. However, we can also think of the standard deviation as a unit of measure of relative distance from the mean in a unimodal, symmetric distribution.

Suppose you had a perfectly symmetric, unimodal distribution. It would look like the well-known bell curve. Of course, in the real world, nothing is perfect. But in statistics, we talk about  ideal distributions, known as "models." Real-life datasets can only approximate the ideal model...but we can apply many of the traits of models to them.  

So let's talk about a perfectly symmetric, bell-shaped distribution for a bit. We call this model a Normal distribution, or Normal model. Because we're dealing with perfection, the mean and median are at the same point. In fact, there are an infinite number of Normal distributions with a particular mean. They only differ in width. Below are some examples of Normal models.
Notice that their widths differ. Another word for "width" is "spread"...which brings us back to Standard Deviation! Take a look at the curves above. In the center section, the shape looks like an upside down bowl, whereas the outer "legs" look like part of a right-side-up bowl. Now imagine the point at which the right-side-up parts meet the upside-down part. Look below for the two blue dots in the diagram. (P.S. They are called "points of inflection," in case you were wondering.)

As shown above, if a line is drawn down the center, the distance from that line to a blue point is the length of one standard deviation. Can you see which lengths of standard deviations in the earlier examples are larger? Smaller?

So, there are two measures that define how a particular Normal model will look: the mean and the standard deviation.

I'd be remiss if I didn't tell you that there is a formula for numerically finding the standard deviation. Luckily, there's a lot of technology out there that automatically computes this for you. (I showed you how to do this in MS-Excel in an earlier post.)

Suppose you have a list of "n" data values, and when you look at a histogram of these values, you see that the distribution is unimodal and roughly symmetric. If we call the values x1, x2, x3, etc. We compute the mean (average, remember?) and note it as x with a bar over it. Then the formula is:

What does the ∑ mean? Let's take the formula apart. First, you are finding the difference between each data value and the mean of the whole dataset. You're squaring it to make sure you're dealing only with positive values. The ∑ means you should add up all those positive squared answers, one for each value in your dataset. Once you have the sum, you divide by

(n-1), which gives you an average of all the squared differences from the mean. This measure (before taking the square root) is called the variance. When you take the square root, you have the value of the standard deviation. So, you see, the standard deviation is the square root of the squared differences from the mean.

Well, that's a lot to digest, so I'll continue with the properties of the Normal model in my next post.