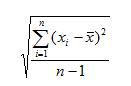More About Standard Deviation: The Normal Distribution

I've haven't said a lot about Standard Deviation up to now: not much more than the fact that it's a measure of spread for a symmetric dataset. However, we can also think of the standard deviation as a unit of measure of relative distance from the mean in a unimodal, symmetric distribution.

Suppose you had a perfectly symmetric, unimodal distribution. It would look like the well-known bell curve. Of course, in the real world, nothing is perfect. But in statistics, we talk about  ideal distributions, known as "models." Real-life datasets can only approximate the ideal model...but we can apply many of the traits of models to them.  

So let's talk about a perfectly symmetric, bell-shaped distribution for a bit. We call this model a Normal distribution, or Normal model. Because we're dealing with perfection, the mean and median are at the same point. In fact, there are an infinite number of Normal distributions with a particular mean. They only differ in width. Below are some examples of Normal models.
Notice that their widths differ. Another word for "width" is "spread"...which brings us back to Standard Deviation! Take a look at the curves above. In the center section, the shape looks like an upside down bowl, whereas the outer "legs" look like part of a right-side-up bowl. Now imagine the point at which the right-side-up parts meet the upside-down part. Look below for the two blue dots in the diagram. (P.S. They are called "points of inflection," in case you were wondering.)

As shown above, if a line is drawn down the center, the distance from that line to a blue point is the length of one standard deviation. Can you see which lengths of standard deviations in the earlier examples are larger? Smaller?

So, there are two measures that define how a particular Normal model will look: the mean and the standard deviation.

I'd be remiss if I didn't tell you that there is a formula for numerically finding the standard deviation. Luckily, there's a lot of technology out there that automatically computes this for you. (I showed you how to do this in MS-Excel in an earlier post.)

Suppose you have a list of "n" data values, and when you look at a histogram of these values, you see that the distribution is unimodal and roughly symmetric. If we call the values x1, x2, x3, etc. We compute the mean (average, remember?) and note it as x with a bar over it. Then the formula is:

What does the ∑ mean? Let's take the formula apart. First, you are finding the difference between each data value and the mean of the whole dataset. You're squaring it to make sure you're dealing only with positive values. The ∑ means you should add up all those positive squared answers, one for each value in your dataset. Once you have the sum, you divide by

(n-1), which gives you an average of all the squared differences from the mean. This measure (before taking the square root) is called the variance. When you take the square root, you have the value of the standard deviation. So, you see, the standard deviation is the square root of the squared differences from the mean.

Well, that's a lot to digest, so I'll continue with the properties of the Normal model in my next post.

Picturing Quantitative Data

Just in case you didn't read the post "Picturing Categorical Data," here's a tiny bit of rehash: The first thing to note that different types of data are pictured in different ways. You might recall from an earlier posting that there are two types of data:

• Quantitative data are numbers for which it makes sense to do arithmetic on them. For example, test scores, dollars, miles, etc. it is meaningful to, say, find their average. Quantitative data usually have labels.
• Categorical data are sub-levels of variables that you do not combine with arithmetic. You usually count them. Examples: eye colors (bllue, brown, green, hazel), education levels (high school, undergrad, graduate, etc.). Some categorical variables are numbers, but not ones that make sense to add; examples are zip codes, numbers on athletic jerseys, phone numbers.

This posting deals with quantitative data only. We deal twith categorical data in an earlier post.

There are many ways to picture quantitative data, but let me introduce two that are most used: the boxplot and the histogram. In both cases, let's use the following set of scores, which are arranged in descending order.

98	86	81
95	86	75
92	86	75
91	85	75
91	82	74
90	82	73
89	81	72

  
Boxplots

(Self-Test): In the earlier post, entitled "Percentiles and Quartiles," we discussed the 5 number summary, consisting of which 5 measures?                                            
(Answer): the minimum, the 1st quartile (Q1), the median, the 3rd quartile (Q3), and the maximum.

A boxplot uses these 5 numbers, arranged on a number line according to their values. As we discussed, each of the four regions marked off by these 5 numbers contain 1/4 of the values in the data set, even if they don't have the same width.

There are 21 numbers shown above. The minimum is 72 and the maximum is 98. Since the number are arranged numerically, we can count to the 11th number to find the median: 85.

We now have 10 numbers on each side of the median. The 1st and 3rd quartiles are the medians of the lower 10 and upper 10 numbers, respectively. Q1 is 75, and Q3 is midway between 90 and 91. Remember: just look between the 5th and 6th number from the bottom and the top in each case.

So, our 5-number summary is: 72 (min), 75 (Q1), 85 (median), 90.5 (Q3), and 98 (max). To make a boxplot, draw a number line that stretches from, say, 70 to 100 and place the 5 numbers in their proper places. Then draw a box around the middle 3 numbers to show the span of the middle 50% of the number set:

A boxplot is helpful not only to see the spread of the data set, but also to see the symmetry of the data. For example, the stretch between the minimum and the median is about the same size as the stretch between the median and the maximum, which tells us that the mean lines up pretty well with the median. (Recall that it doesn't always end up this way!) The unevenness of the outer regions (which we call the "whiskers") are uneven, telling us that the data looks more heavily weighted toward the low side of the number line. If the boxplot looked like the following, the data would be roughly symmetric:

Symmetry in a data set is important to recognize, because we can assume other important traits. More about this in a future post.

Now, if a data set has outliers, they are shown with a symbol; for instance, a star:

In cases like this, a new maximum that lies within the boundary for outliers is determined.  As I said in a previous post, you should look for possible reasons for outliers.

Histograms

A histogram tracks the number of observations (like the values in the above table) that lie within consecutive, same-width intervals on a number line. While most people do not make histograms by hand, we'll go through how it's done so you can understand what a histogram looks like. In statistics histograms are used heavily; usually to see the shape of the data distribution.

Start by examining the data values. They range from 72 to 98, and the range (as defined in statistics) is 98 - 72 or 26. We want to divide 26 into a number of equal-sized intervals, then find out how many of the numbers in the data set lie in each interval. We will represent that number as the height of that interval's bar.

How many intervals do we need? Well, to me, that's a "squishy" question. You want enough to be able to see a shape, but not so many that you hardly have any values in each interval. A rule of thumb that I use is between 6 and 8. Because our range is 26, I'm going to use 7 for intervals, because 7*4 is 28, which is closer to 26 than a multiple of 6 or 8. So we have the following number line. Each interval will be 4 units wide (again, because 7*4 is 28), so I've numbered the line accordingly.

(Self-Test): What's with the // on the number line above?
(Answer): Number lines should always be to scale, but in this case a number line going from 0 to 100 probably wouldn't fit on the page. So, I use the // to indicate a break in the numbering.

Now I need to make a small decision: Shall I count the labelled numbers as the start or the end of the interval? It doesn't matter, just as long as you're consistent. I'm going to count the numbers as the start of each interval. So, my first interval will go from 72 to 75; my second will be from 76 to 79, and so on.

For each interval, you need to count how many values in the data set fall within that interval. For example, there are 6 numbers that are between 72 and 75, inclusive. So the height of my bar for the first interval will be 6 units high.

Our second interval, which goes from 76 to 79, has no values. So we leave a space to show that zero values are in that interval. The next interval goes from 80 to 83, and there are four values that lie in that interval. So, the bar will be 4 units high.

Continuing on for the rest of the intervals, here is our finished product:

This histogram has an interesting shape. If the dataset represents grades, we can assume that there 6 out of 21 "C" students, while twice that many are in the "B" to "A-" range. I'll be saying more about shapes of distributions in a later post. For now, suffice it to say that the shape of a distribution is an important thing to assess when you're looking at data.

The Center: Mean, Median, and Mode

Let's begin with what might be familiar territory: how people describe a list of numbers (data!) using a single central measure. There are three of these numbers -- mean, median, and mode -- and which one is best heavily depends on the data you're describing. Let's go over how to determine each of these measures, and discuss the pros and cons of each.

Consider the following very short list of test grades one of my students received last semester: 74, 84, 88, 71, and 88.

• To find the mean (also known as the average): just add up all of the numbers and divide by how many numbers are in the set. That is: (74+84+88+71+88) divided by 5 = 405 / 5 = 80. The symbol we'll use for the mean is

         The mean is good to use when there are no extreme values (numbers that lie far
         outside the span of the other numbers. There are none in this set of numbers, so 
         we say there are no outliers and so the mean is just fine to use. 

• To find the median (also known as the midpoint), arrange the grades in numerical order: 71 ,74, 84, 88, 88. Note that we list duplicates as many times as they occur. Once the numbers are arranged, find the number that's in the middle of the list. In this short list, it's 84.

         Now, what if there is no middle number? For example, suppose we add a sixth   
         score: 94. We now have the list, in order: 71, 74, 84, 88, 88, 94. When we look  
         for the middle,there isn't a single score but two: 84 and 88. In this case, find the  
         average of these two numbers: (84+88}/2 = 86.

         The median is good to use almost anytime, but is especially important to use when
         there are outliers. To see why the median is more accurate than the mean as a
         central measure when there are outliers, think about the salaries of a very small
         company, from the line workers to the CEO:

                 Line worker 1:       $  28.000
                 Line worker 2:       $  32,500
                 Line worker 3:       $  33,100
                 Supervisor:           $  45,000
                 Marketing person: $  62,300
                 Sales person:        $  70,000
                 CEO:                    $175,000

         Compare the mean ($ 63,700) to the median $45,000. The mean isn't realistic    
         because 5 out of 7 of the workers are making less! This is because the outlier,
         $175,000, inflates the calculation of the mean. On the other hand, the median is
         much more reflective of the central salary: 3 employees make more, 3 make less.

• Finding the mode is easy, but it exists only if there are duplicates in the list. Simply find the number that occurs the most. In our original list of 5 test scores, 88 occurs twice, so the mode is 88. In our salary example directly above, there is no mode because no salary occurs more than once. If one number occurs twice and another number occurs four times, the latter is the mode because it occurs the most.

        The mode is probably the least useful as a measure of center. The only time it 
        makes sense is if there are many occurrences of the same number, compared to   
        the number of other values. Example: 57, 66, 75, 75, 75, 75, 75, 75, 82.

Moral of the Story: When you see the terms "mean" and "median" used in articles, do not assume that the writer is always using the right term. If you see the data, you can check this. Otherwise, the author might be confusing one measure for the other. Not everyone understands the difference, but now (hopefully) you do!

Self quiz: What are the measures of center (mean, median, and mode) for the following list of 8 student scores? 43, 77, 66, 73. 85, 75, 92, 81.

(Answer): Mean = 74; Median = 76; Mode = none. Which is the better measure? Technically, the median would be better because the low score of 43 is dragging the mean down a bit. However, it's pretty much a wash since the mean and median are so close to each other.